百問繚乱では、分数やルート、文字式等、中学数学程度の数式を自動で採点する機能があります。
また、(x-1)(x-2)と(x-2)(x-1)のどちらでも正解にする、OR採点機能もあります。
この記事では、その設定方法について説明します。
公式に提供されている百問繚乱のマニュアルには次のように記載されています。
2桁以上の数字・正負符号・分数・平方根(ルート)・簡易な文字式・カッコや不等号などの記号といった、中学数学程度の数式を自動採点する機能です。
この中学数学程度の数式を「簡易に複合したもの」も自動で採点することができます。
- 数式の自動採点設定の方法
- (x-1)(x-2)と(x-2)(x-1)のどちらでも正解にする方法(OR採点)
- 採点精度
- 文系科目での活用方法
設定方法
数式の認識
解答欄の枠が作成されたところから説明します。
解答欄の枠作成についてはこの記事を参考にしてください。
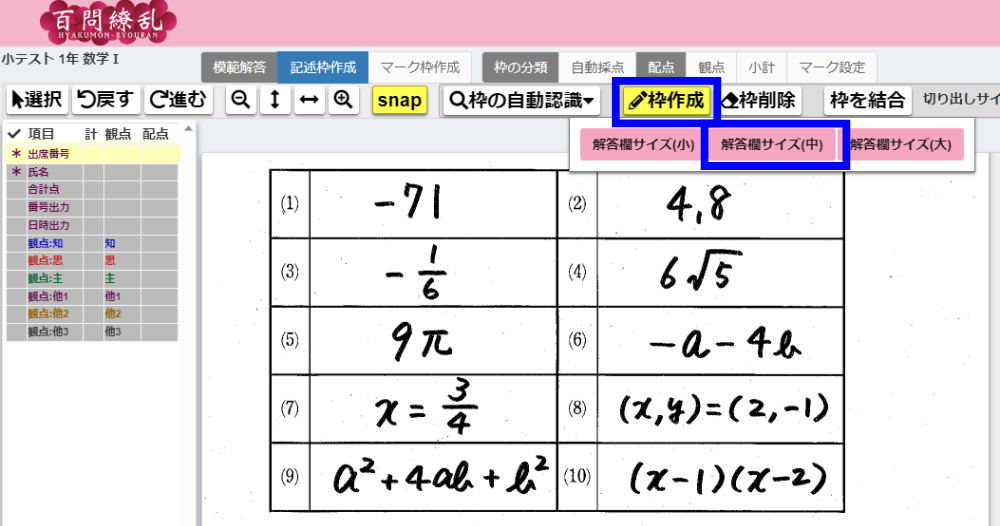
「自動採点」タブにある「数式」をクリックしてから、解答欄をクリックすると模範解答の数式を認識し始めます。
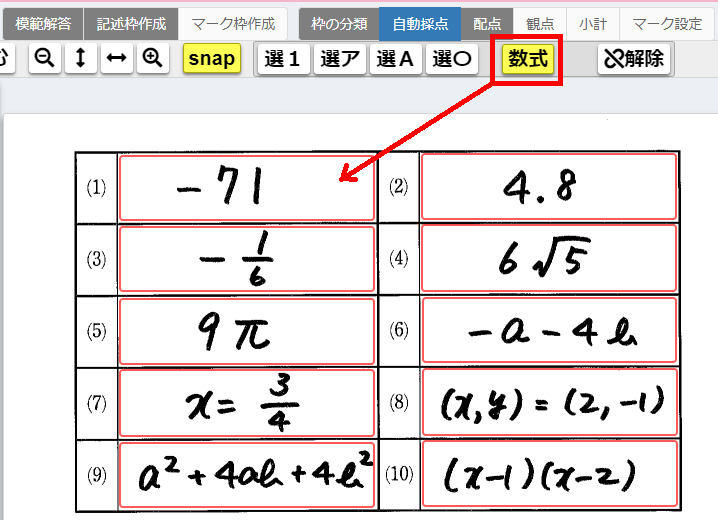
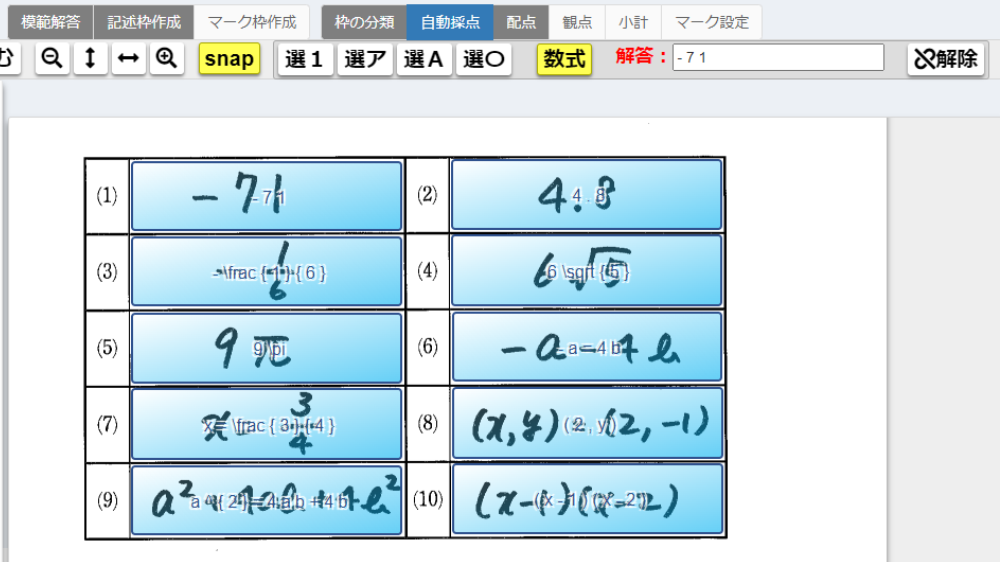
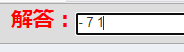
認識結果が「解答:」の欄に表示されます。必要に応じて半角で修正してください。


枠内に書かれた認識しやすい文字であれば、正確に読み取ってくれます。
記号と記号の間に半角スペースが入りますが、なくても構いません。
たまに「ー」と「=」を間違えることがあります。
「解答:」の欄の数式を修正した後、さらに数式を修正したい場合
そのまま該当の解答欄をクリックすると、再度数式を認識して、はじめに修正したものが消えてしまします。
こういった場合は、「選択」をクリックしてボタンを黄色にしてから、
水色の解答欄をクリックします。

すると数式を認識せず、今入力されている数式を修正することができます。
(x-1)(x-2)と(x-2)(x-1) OR採点
(10) について、(x-1)(x-2) と (x-2)(x-1) を両方正解にしたい場合は、この2つを「$」でつなげてください。
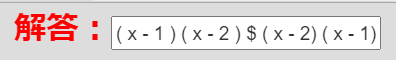
式A、式Bどちらも正解にしたいときは
式A $ 式B
加えて、式Cでも正解にしたいときは
式A $ 式B $ 式C
のように正解にしたい式を「$」でつなげてください。
TeXで記述
以下の式や記号は、TeX(テフ)コマンドで入力します。
| 記号 | TeXコマンド |
|---|---|
| °(角度の度) | ¥circ |
| 分数 | ¥frac { 分子 } { 分母 } |
| ≦ | ¥leqq |
| π(パイ) | ¥pi |
| ルート | ¥sqrt { ルートの中 } |
| θ(シータ) | ¥theta |
| ±(プラスマイナス) | ¥pm |
| 指数(aの2乗) | a ^ 2 |
対応している解答の形式
| 形式 | 例 |
|---|---|
| 整数 | 13 や -13 や 12+13 |
| 小数 | 3.5 や -3.5 や 3.5+2.9 |
| 分数 | ¥frac{1}{3} や -¥frac{1}{3} |
| 平方根 | ¥sqrt{5} や 3¥sqrt{5} |
| 比 | 3:5 |
| 数字+アルファベット | 3x や 3x+2y |
| 数字+アルファベットの分数 | ¥frac{3x}{2} |
| 数字+アルファベットの等式 | x=5 や y=2 |
| カンマ区切りの数字+アルファベット | x=2,5 |
| カッコ付きの数字+アルファベット | (x+1)(x-3) |
| 指数付きの数字+アルファベット | x^{2}-4x+4 |
| 上記の簡易な複合 | x=¥frac{3y}{2} |
「簡易な複合」とはどの程度か後半でいくつか検証しました。
対応している記号やアルファベット
以下の記号とアルファベットの一部を認識できます。
| 記号 | アルファベット | |
|---|---|---|
| -(ハイフン) | A | h |
| ,(カンマ) | B | i |
| .(ピリオド) | C | k |
| :(コロン) | D | m |
| ( | L | n |
| ) | a | r |
| + | b | t |
| < | c | x |
| = | g | y |
認識の精度(簡易な数式)
気になる認識の精度ですが、簡易な数式は高い精度で認識することができました。
次の表は、設定方法で示した解答用紙を16件認識させた結果です。
| ○→✕と修正した数 | ✕→○と修正した数 | |
| (1) -71 | 0 件 | 1 件 |
| (2) 4.8 | 0 件 | 1 件 |
| (3) -1/6 | 0 件 | 1 件 |
| (4) 6√5 | 0 件 | 0 件 |
| (5) 9π | 0 件 | 0 件 |
| (6) -a-4b | 0 件 | 0 件 |
| (7) x=3/4 | 1 件 | 0 件 |
| (8) (x,y)=(2,-1) | 0 件(全て✕で認識) | 11 件 |
| (9) a^2+4ab+b^2 | 未計測 | 未計測 |
| (10) (x-1)(x-2) | 0 件 | 3 件 |
結果の詳細です。
(1)から(10)について、<自動採点直後>と<修正後>の画面を比較しました。
(1)
<自動採点直後>
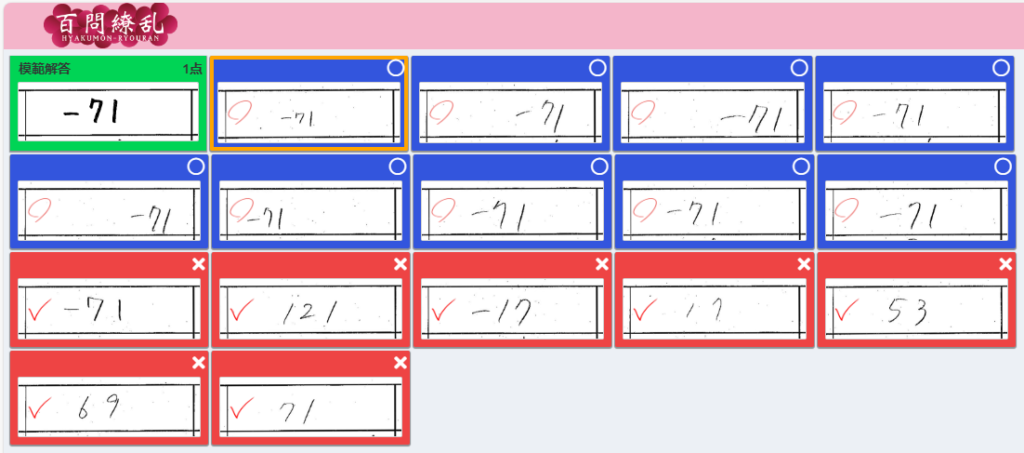
<修正後> 【 ○→✕ 0件 】【 ✕→○ 1件 】
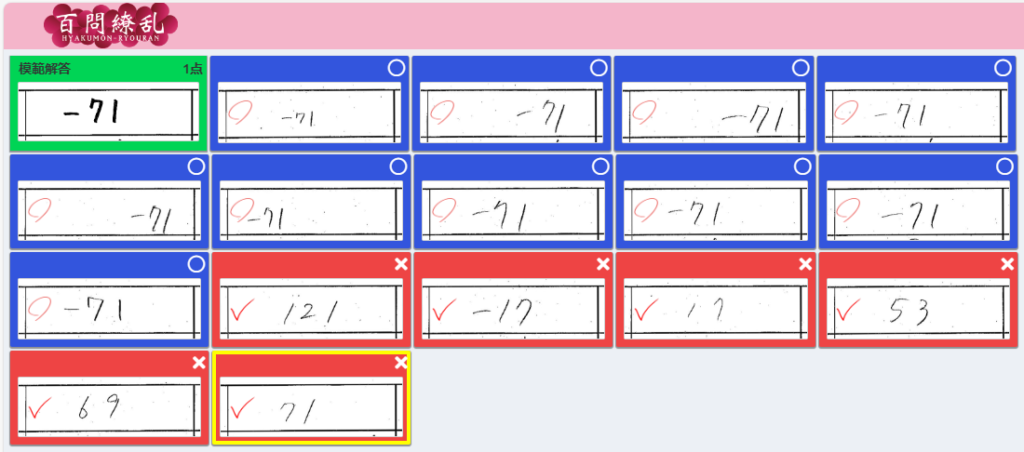
(2)
<自動採点直後>
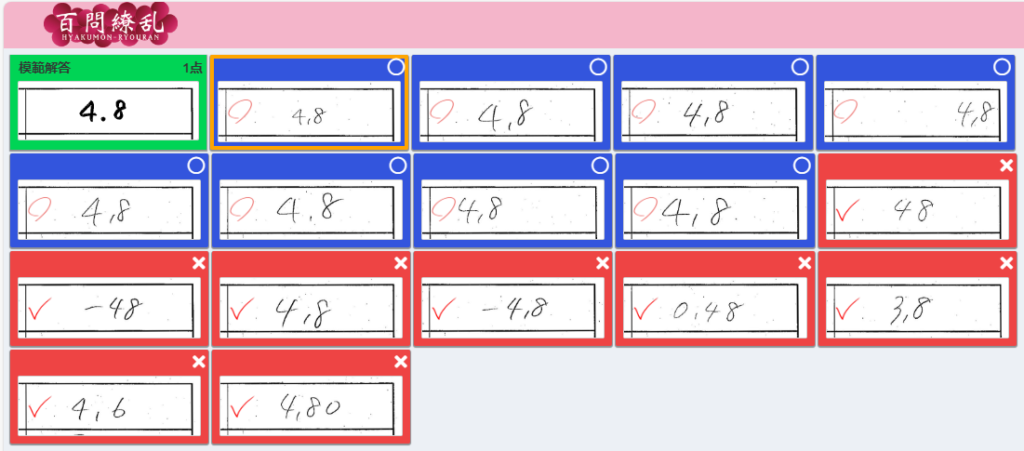
<修正後> 【 ○→✕ 0件 】【 ✕→○ 1件 】
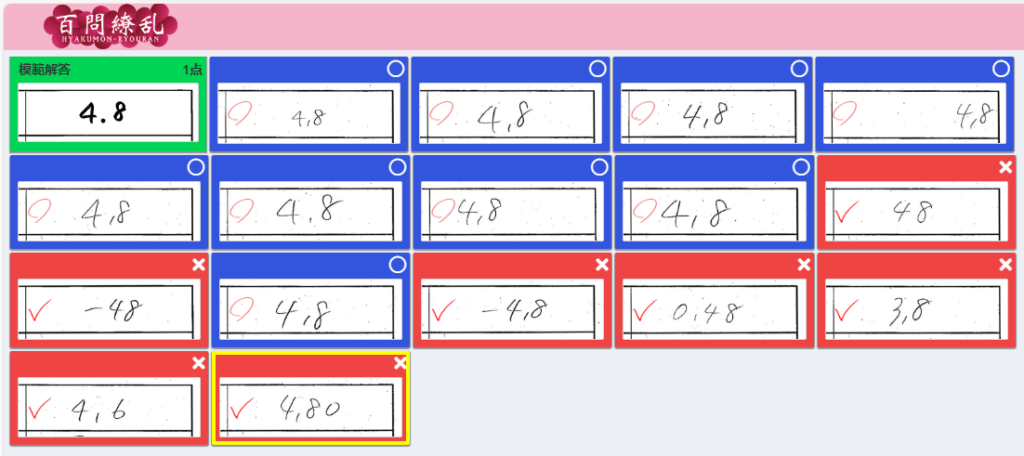
(3)
<自動採点直後>
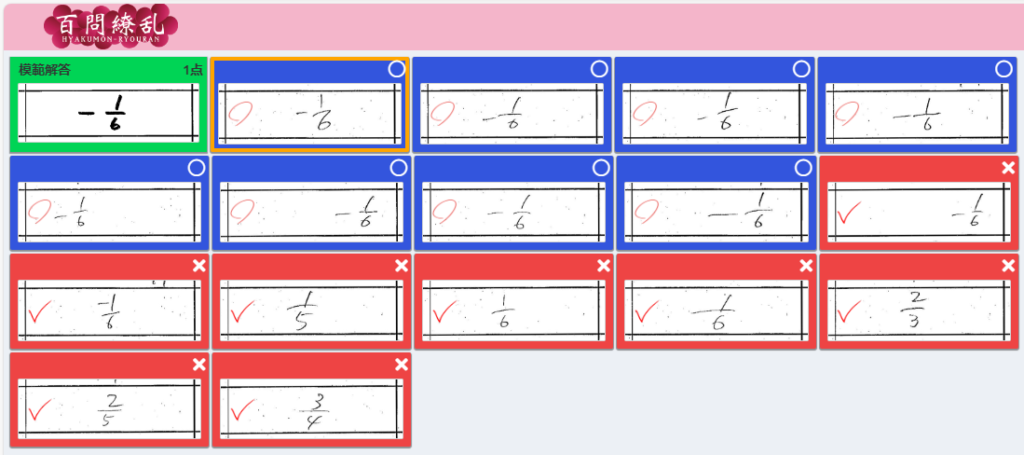
<修正後> 【 ○→✕ 0件 】【 ✕→○ 1件 】
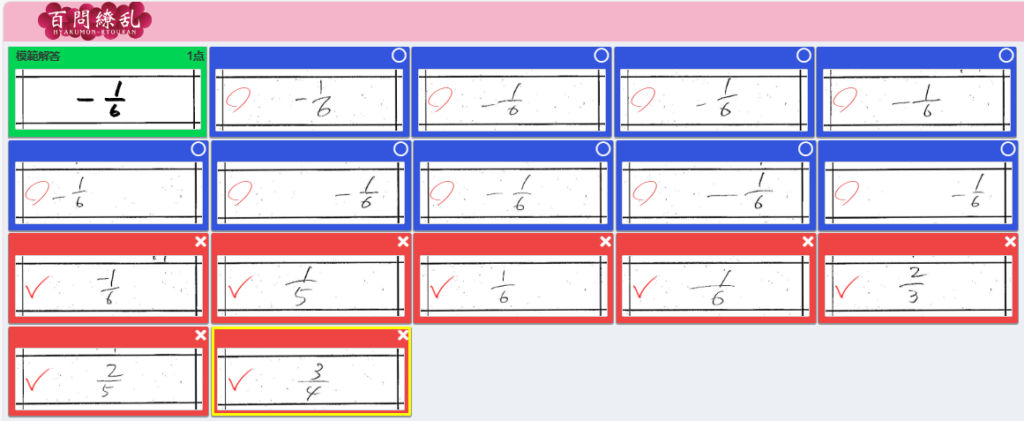
(4)
<自動採点直後> 修正なし【 ○→✕ 0件 】【 ✕→○ 0件 】
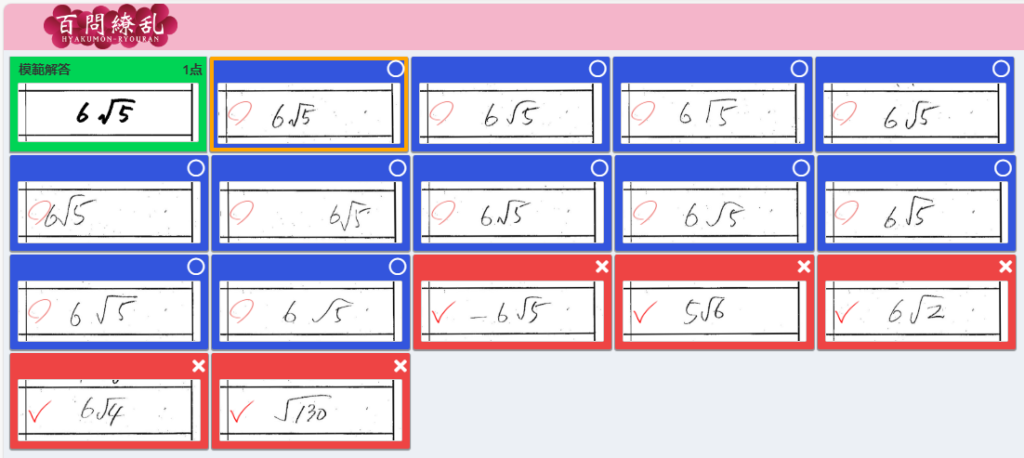
(5)
<自動採点直後> 修正なし【 ○→✕ 0件 】【 ✕→○ 0件 】
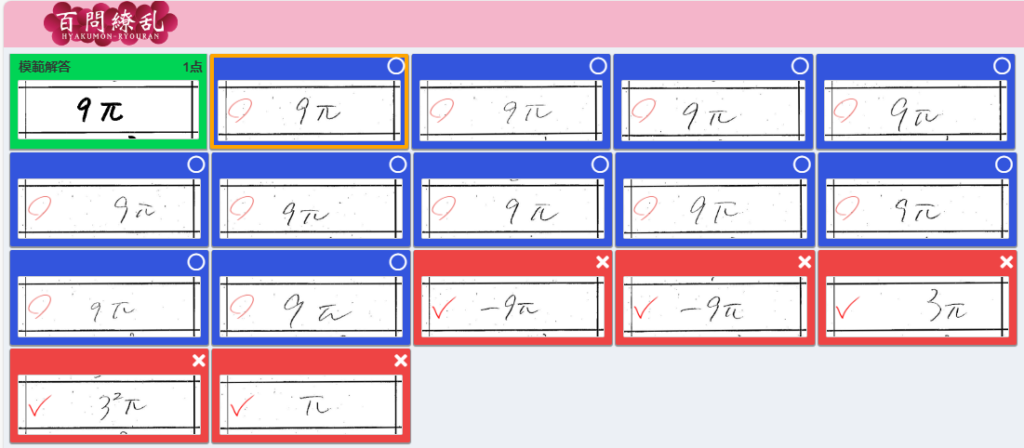
(6)
<自動採点直後> 修正なし【 ○→✕ 0件 】【 ✕→○ 0件 】
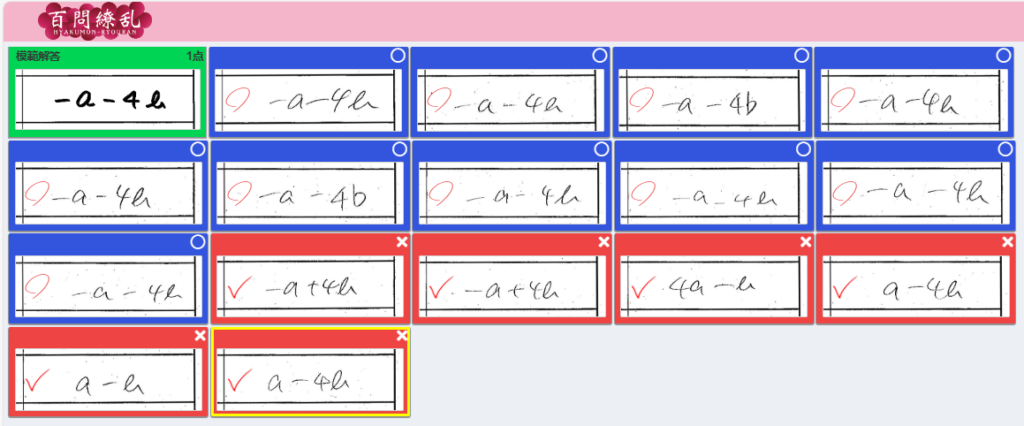
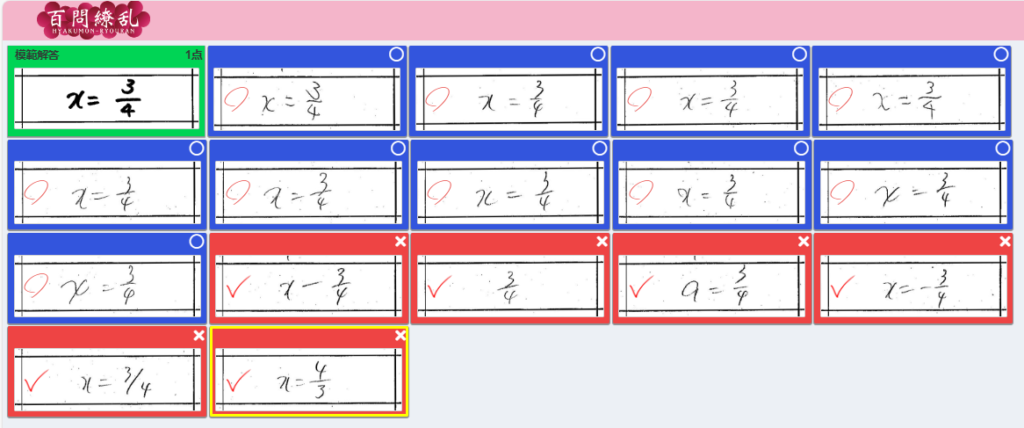
(7)
<自動採点直後>
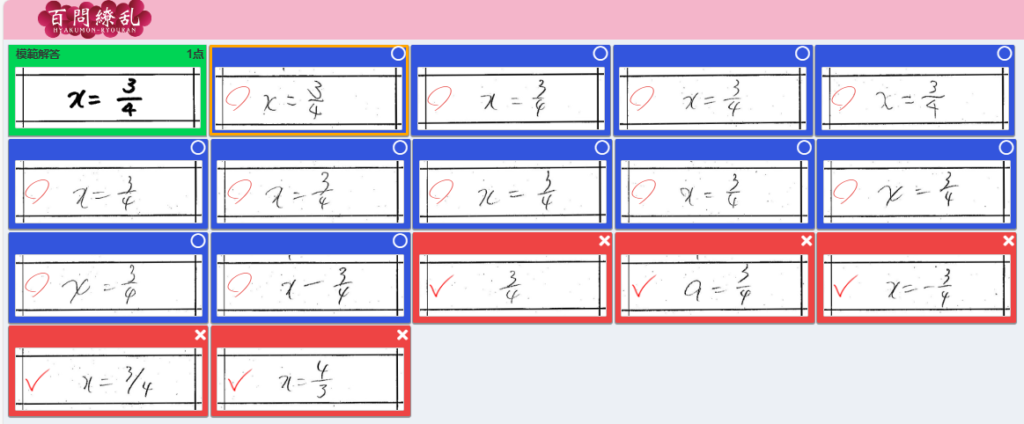
<修正後> 【 ○→✕ 1件 】【 ✕→○ 0件 】
マイナス「ー」をイコール「=」と認識したようです。
(8)
<自動採点直後>
○と認識されたものはありませんでした。
この形は、マニュアルにある「簡易な数式の複合」ではないかもしれません。

<修正後> 【 ○→✕ 0件 】【 ✕→○ 11件 】

(10)
<自動採点直後>
(x-1)(x-2) と (x-2)(x-1) を両方正解にしていることがわかります。

<修正後> 【 ○→✕ 0件 】【 ✕→○ 3件 】

認識の精度(複雑な数式)
簡易な数式を組合わせた複雑な数式について、39件の解答用紙を認識させた結果です。
<自動採点直後>
2次方程式を解の公式で解く問題です。○と認識されたものはありませんでした。
分母や分子に「+」「-」があるこの形は「簡易な数式の複合」ではないかもしれません。

<修正後> 【 ○→✕ 0件 】【 ✕→○ 20件 】
指定した数式が認識できるかを判断したかったので、今回は「±」で書かれたものだけを正解としました。「+」と「ー」を分けて書いたものは不正解としています。

<自動採点直後>
不等式を「,」カンマで区切った式です。
○と認識されたものがあるということは、この形は認識できるレベルという事でしょう。

<修正後> 【 ○→✕ 0件 】【 ✕→○ 6件 】
正誤で並び替えたとき、誤と判断されたもの中でも何かの順序で並んでいるようです。
正解と修正するものが続けて現れることがよくあります。

<自動採点直後>
「,」カンマで区切られていない、1つの不等式です。

<修正後> 【 ○→✕ 0件 】【 ✕→○ 1件 】
認識結果は良好でした。この形は精度良く認識できる「簡易な数式の複合」のようです。

裏技?
別の記事でも紹介しましたが、自動採点で認識できる文字は以下のとおりです。
| 文字の種類 | 自動で認識可能 | 文字数 |
| 数字 | 0 ~ 9 | 10文字 |
| カタカナ | ア ~ チ | 17文字 |
| アルファベット | A ~ F | 6文字 |
| 記号 | ○ , ✕ | 2文字 |
本来の趣旨とは違いますが、数式の自動採点機能を使うことで、こんなこともできます。
選択肢として単独の数字「 0 〜 9 」を認識できた。数式自動採点では「 10 」以降も認識できるので、選択肢の数を増やせる。
単独のアルファベット「 A 〜 F 」を認識できた。数式自動採点では「 A,B,C,D,L 」を認識できる。これを利用して、
A,B,C,Dの4択問題で正解を2つ選べとした場合に、数式自動採点で次のように設定する。
A,B $ B,A AとBが正解
数式を採点することがあまりない文系科目で活用できる場面があるかもしれません。
おわりに
今回は、百問繚乱で数式を自動で採点する方法を紹介しました。
数式を自動採点する機能があるのは今のところ百問繚乱だけではないかと思います。
また、
式A $ 式B
と設定すればOR採点ができるので、数式を採点する際に効率化が図れます。
ちなみに、この方法は公式のマニュアルに載ってませんでした。参考にしてください。
また使ってみて疑問に思ったことや実現すると素敵だなと思ったことは、
- 「簡易な数式の複合」とは具体的にどの程度か
- 「2次方程式の解」程度の数式を認識してほしい…
- 「解答:」の欄が長くなると、「$」を入れたとき見やすい
- アルファベットの種類を大文字だけでもいいので、もう少し増やす
細かいこと言うとキリがありませんが、そもそもこの機能は、数式を採点する教科の方にとって革命的だと感じました。ありがとうございます。
最後までご覧いただきありがとうございました。



コメント